机器学习系统设计笔记9--降维

最近看完了 Willi Richert的《机器学习系统设计》。书虽然有点薄但也比较全，内容感觉有点偏文本处理，里面介绍了一些文本处理的方法和工具。综合起来看作为机器学习入门还是挺不错的，这里就简单记一下我做的笔记，方便回顾。书中的代码可以通过它说到的网站下载，这里是第9部分笔记。

第十一章降维

为什么要进行降维？

多余的特征会影响或误导学习器。并不是所有机器学习方法都有这种情况（例如，支持向量机就喜欢高维空间），但大多数模型在维度较小的情况下会比较安全。
另一个反对高维特征空间的理由是，更多特征意味着更多参数需要调整，过拟合的风险也越大。
我们用来解决问题的数据的维度可能只是虚高。真实维度可能比较小。
维度越少意味着训练越快，更多东西可以尝试，能够得到更好的结果。
如果我们想要可视化数据，就必须限制在两个或三个维度上，这就是所谓的数据可视化。

降维方法大致分为特征选择法和特征抽取法。特征选择利用一些统计方法（相关性和互信息量）在大特征空间中进行特征选择的方式。而特征抽取试图将原始特征空间转换为一个低维特征空间。

特征选择

为了能够得到更好的机器学习结果，输入的特征相互之间应该没有依赖关系，同时又跟预测值高度相关。这意味着，每个特征都可以加入一些重要信息。把它们之中的任何一个删掉都会导致性能下降。

筛选器选择

筛选器试图在特征丛林中进行清晰，它独立于后续使用的任何机器学习方法。它基于统计方法找出冗余或无关特征。

1.相关性

通过使用相关性，我们很容易看到特征之间的线性关系，这种关系可以用一条直线来拟合。相关系数$Cor(X_1,X_2)$是用皮尔逊相关系数（Pearson correlation codfficient）计算出来的（皮尔逊r值），采用scipy.stat里的pearsonr()函数计算

1
2
3

>>> from scipy.stats import pearsonr
>>> pearsonr([1,2,3], [1,2,3,1])
(0.99962228515,0.01749809681)

2.互信息

对于非线性关系，仅用相关性来检测是不幸的，这里使用互信息来进行选择，互信息会通过计算两个特征所共有的信息，与相关性不同，它依赖的不是数据序列，而是数据的分布。要理解它是怎样工作的，我们需要深入了解一点信息熵的知识。

假设我们有一个公平的硬币，在旋转它之前，它是正面还是反面的不确定性是最大的，因为两种情况都有50%的概率，这种不确定性可以通过克劳德.香农（Claude Shannon）的信息熵来衡量：

$$H(X) = -\sum{n}{i=1}p(X_i)log_2p(X_i)$$

在公平硬币情况下，令$x_0$代表硬币正面，$x_1$代表硬币反面，$p(X_0)=p(X_1)=0.5$

因此我们有：

$$H(X)=-p(x_0)log_2p(x_0)-p(x_1)log_2p(x_1)=-0.5\cdot log_2(0.5)-0.5\cdot log_2(0.5)=1.0$$

现在想象以下我们事先知道这个硬币实际上是不公平的，旋转后肯呢个由60%的概率是硬币的正面：

$$H(X)=-0.6\cdot log_2(0.6)-0.4\cdot log_2(0.4)=0.97$$

可以看到在这种情况结果开始偏移1，不管是概率往哪边偏移，不确定性都会远离我们在0.5时得到的熵，到达极端的0值，如下图。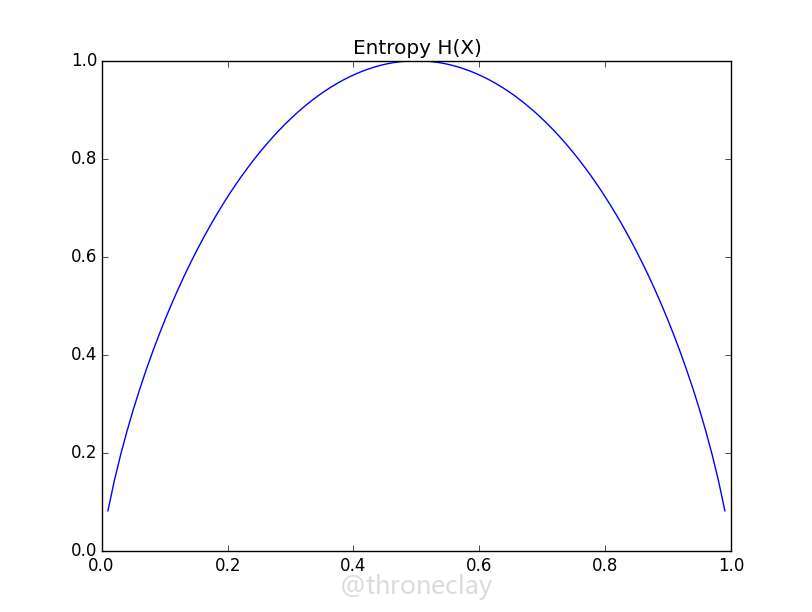

我们现在修改其计算方式，使之能够应用到2个特征上而不是上面的一个。它衡量了在知道Y的情况下，X中所减少的不确定性。这样我们就得到一个特征使另一个特征的不确定性减少的程度。例如我们现在知道外面的草地是湿的，那么这种不确定性就会减少。

更正式地说，互信息量是这样定义的：

$$I(X;Y)=\sum{m}{i=1}\sum{n}{j=1}P(X_i,Y_i)log_2\dfrac{P(X_i,Y_i)}{P(X_i)P(Y_j)}$$

为了把户型西量限制在$[0,1]$区间，需要把它除以每个独立变量的信息熵之和，然后就得到了归一化后的互信息量：

$$NI(X;Y)=\dfrac{I(X,Y)}{H(X)+H(Y)}$$

我们计算每一对特征之间的归一互信息量。对于具有较高互信息量的特征对，我们会把其中一个特征扔掉。在进行回归的时候，我们可以把互信息量非常低的特征扔掉。不过对于较小的特征集合这种方式的效果或许还可以，但对于大特征集合，这个过程会非常缓慢，因为我们计算的是每对特征之间的互信息量！

筛选器还有一个巨大缺点，它们扔掉在独立使用时没有用处的特征。但实际情况往往是，一些特征看起来跟目标变量完全独立，但当他们组合在一起的时候就有效用了。要保留这一类特征，我们需要封装器。

封装器选择

筛选器对删除无用特征有很大的作用，但仍然可能有一些特征，它们之间彼此独立，并和目标变量有一定程度的依赖关系，但从模型角度看，它们毫无用处，例如某几个特征跟结果是XOR(异或)关系。

在sklearn.feature_selection包中有各种优秀的封装器类。这个领域的一个真正的主力军叫做RFE，这个缩写代表的是特征递归消除（recursive feature elimination）。它会把一个估算器和预期数量的特征当作参数，然后只要发现一个足够小的特征子集，就在这个特征集合里训练估算器。RFE实例在封装估算器同时，它本身看起来也像一个估算器。下面一个例子中，我们通过datasets的make_classification()函数，创建了一个人工构造的分类问题，它包含100个样本，10个特征，其中只有3个对解决问题有价值：

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

from sklearn.datasets import make_classification

X, y = make_classification(
    n_samples=100, n_features=10, n_informative=3, random_state=0)

clf = LogisticRegression()
clf.fit(X, y)

for i in range(1, 11):
    selector = RFE(clf, i)
    selector = selector.fit(X, y)
    print("%i\t%s\t%s" % (i, selector.support_, selector.ranking_))

当然，真实情况下，我们需要知道我们设置的n_features_to_select的正确值，但是事实证明，n_features_to_select并不需要特别精确，在不同的n_features_to_select值下，support_和ranking_的值变化并不大。

对于像决策树这样拥有深植于其内核的特征选择机制，就不需要进行特征选择了，是否使用特征选择一是看你的数据特征数量，二是看选用的机器学习算法。

特征提取

从某种程度上说，我们删掉冗余特征和无关特征后，经常还有很多特征，采用特征提取的方法能起到对特征空间重构的效果，使我们更容易接近模型，或者把维度砍到二维或者三维，实现数据的可视化。

PCA和LDA

主成分分析（PCA），通常是你想要删减特征但又不知道用什么特征抽取方法时，第一个要去尝试的方法。PCA的能力是有限的，因为它是一个线性方法。但它很可能足以使你的模型得到很好的结果，加上良好的数学性质，发现转换后特征空间的速度以及在原始和变换后特征间相互转换的能力，成为了一个常用的机器学习工具。

总的来说，对于原始特征空间，PCA会找到一个更低维度空间的线性映射，它的性质有：

保守方差最大
最终的重构误差（从变换后特征回到原始特征）是最小的。

由于PCA只是简单的对输入数据进行变换，它既可以用于分类问题，也可以用于回归问题。

PCA的基础算法可以用下面几步来描述：

从数据中减去它的均值；
计算协方差矩阵；
计算协方差矩阵的特征向量。

如果我们从N个特征开始，这个算法会返回一个变换后的N维特征空间。矩阵的特征值预示着方差的大小，这是通过对应的矩阵特征向量来描述的。在应用中的场景类似这样：假设我们由N=1000个特征，然后我们从中挑选出20个具有最高矩阵特征值的特征向量。

举一个人造数据集的例子：

from numpy as np
from sklearn import decomposition

np.random.seed(3)
x1 = np.arange(0, 10, .2)
x2 = x1 + np.random.normal(loc=0, scale=1, size=len(x1))
X = np.c_[(x1, x2)]
good = (x1 > 5) | (x2 > 5) # 一些任意的类别
bad = ~good  # 使得示例看起来比较好

# sklearn中封装了pca的计算，通过n_components可以指定想要多少维特征
pca = decomposition.PCA(n_components=1)

# 使用pca的fit来分析数据，并将数据映射到变换后的特征空间中
Xtrans = pca.fit_transform(X)

# 重构误差，这是在变换中保留下来的数据方差。
print(pca.explained_variance_ratio_)

当然情况并不是这么简单，初始化pca时往往不会指定n_components参数，而是让他进行完全转换，对数据进行拟合后，explained_variance_ratio_包含了一个降序排列的比例数组。第一个值就是描述最大方差防线的基向量的比例，而第二个值就是次大方差方向的比例，以此类推。画出这个数组后，我们可以快速看到我们需要多少个成分：在图表里成分个数恰好出现拐角的地方，通常是一个很好的猜测。

成分个数和方差之间的关系图，叫做Scree图，在http://scikit-learn.sourceforge.net/stable/auto_examples/plot_digits_pipe.html 里可以下到一个结合Scree图和网格搜索来维分类问题寻找最佳设置的例子

PCA的局限主要在处理非线性数据时，这时候可以用 线性判别式分析(Linear Discriminant Analyisis, LDA) ，这个方法试图让不同类别样本之间的距离最大，同时让相同类别样本之间的聚类最小，一个简单的例子告诉你怎么用：

1
2
3

from sklearn import lda
lda_inst = lda.LDA(n_components=1)
Xtrans = lda_inst.fit_transform(X,good)

注意，PCA是一个无监督的特征抽取方法，而LDA是一个有监督的方法，我们给fit_transform()方法提供了类别标签。

多维度标度 MDS

MDS跟PCA都是特征提取方法，两个的区别在于，PCA试图对保留下来的数据方差进行优化，而MDS在降低维度的时候试图尽可能保留样本间的相对距离。当我们有一个高维数据集，并希望获得一个视觉印象的时候，这是非常有用的。

MDS对数据点本身并不关心，它对数据点间的不相似性却很感兴趣，并不这种不相似性解释为距离。因此，MDS算法第一件要做的事情就是，通过距离函数$d_0$对所有N个k维数据计算距离矩阵。它衡量的是原始特征空间中的距离（大多数情况下都是欧式距离）

$$ \begin{pmatrix} X_{11} & \cdots & X_{N1} \\ \vdots & \ddots & \vdots \\ X_{1k} & \cdots & X_{Nk} \end{pmatrix} \to \begin{pmatrix} d_0(X_1,X_1) & \cdots & d_0(X_N,X_1) \\ \vdots & \ddots & \vdots \\ d_0(X_1,X_N) & \cdots & d_0(X_N,X_N) \end{pmatrix} $$

现在，MDS试图在低维空间中放置数据点，使得新的距离尽可能与原始空间中的距离相似，由于MDS经常用于数据可视化，所以低维空间的维度大多数时候都是2或者3.

让我们看看下面这个五维空间中包含三个样本的简单数据。

X = np.c_[np.ones(5), 2 * np.ones(5), 10 * np.ones(5)].T

# 使用sklearn的manifold包中的MDS类，先指定把X转换到一个三维空间中，
from sklearn import manifold
mds = manifold.MDS(n_components=3) # 转换成2维的时候修改这里
Xtrans = mds.fit_transform(X)

其实深入了解MDS后，感觉它并不是一个算法，而是一类不同的算法，我们只使用了其中一个而已。流形学习中还有一些其他的降维方法，可以学习学习。

总结

这本书还有第十二章，但跟机器学习算法并没有太大关系，而是讲亚马逊云服务怎么用的，所以就不再写了。机器学习内容非常丰富，想全都学明白不动手写写代码，亲自去实验一下是不行的，所以还是多看代码，多去实验，多找找数据去试着做一做。

机器学习系统设计笔记9--降维

机器学习系统设计笔记9--降维

第十一章 降维

特征选择

筛选器选择

封装器选择

特征提取

PCA和LDA

多维度标度 MDS

总结

第十一章降维