BP算法是深度学习的训练算法，没有好的训练就不可能有好的分类结果，最近看了Martin T. Hagan等著的《神经网络设计》，里面讲的非常清晰，深入浅出，例子也很不错，自己根据里面的十一章给的一个计算例子写出了Matlab代码，这本书也带matlab程序，但其代码充斥着图形界面的代码，动辄上千行，很是难懂，我也懒得看，这里写的这个小代码一是想试试他给的计算过程怎么样，二是也动手写写代码加深下印象。为了能更好的理解细节，这里没有使用Matlab的神经网络库函数，看起来会更清晰。

这个代码的作用是用两层的神经网络逼近在区间［－2，2］间的$1+sin((\pi/4)*p)$函数，p是输入。第一层有两个神经元，第二层有一个神经元。这里用的最原始的BP算法，最速下降版的BP。对于权值和偏置值的调整公式如下：
$$W(k+1) = W(k) - as(m)a(m-1)$$
$$b(k+1) = b(k) - as(m)$$
其中k是指的第几次调整，m是指的层数，第一层到第M层，$a(0)$是输入$a(m)$就是m层的输出了，W是权值，b是偏置值，W的行数是神经元的数量，而列数是$a(m-1)$的维数，b是向量，有多少个神经元，就有多少行。s是敏感度，第m层的计算必须依靠第m＋1层的结果也就有了BP的称呼。其计算公式如下：
$$s(m) = \dfrac{\alpha F}{\alpha n(m)}W(m+1)^T s(m+1)$$
$$s(M) = -2 \dfrac{\alpha F}{\alpha n(m)}(t-a)$$
这里$\dfrac{\alpha F}{\alpha n(m)}$，这个东西计算还是非常麻烦的，他是个$S\times S$的单位矩阵，每行的那一个元素是对当前层对应神经元的传输函数的偏导，他就等于下面的这个矩阵：
$$
\begin{bmatrix}
\dfrac{\alpha f(n(m))}{n(0)} & 0 & \cdots & 0 \\
0 & \dfrac{\alpha f(n(m))}{n(1)} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \dfrac{\alpha f(n(m))}{n(S)}
\end{bmatrix}
$$
其实函数是一样的，只不过不同的维度上的W和b都不同，导致最后计算的值也不同。

下面是我写的Matlab代码，亲测可用，但也确实可以看出，最速下降的这种方式好慢，配有一点注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
% 用两层神经网络逼近从－2到2区间的 1+sin((pi/4)*p)函数，
a=0.01; %学习速率
% 参数
Wx1=random('norm',-0.5,0.5,2,1);
b1=random('norm',-0.5,0.5,2,1);
Wx2=random('norm',-0.5,0.5,1,2);
b2=random('norm',-0.5,0.5);
%BP过程
p=-2.0; %初始的输入向量P
flag=0;
E=0;
while(flag==0)
    % 先正向计算最后结果，计算误差e
    a1=logsig(Wx1*p+b1);
    a2=purelin(Wx2*a1+b2);
    t=1+sin(pi/4*p);
    e=t-a2;
    % 计算两层的偏导数
    f1=(1-a1).*a1;
    f2=1;
    s2=-2*f2*e;
    s1=diag(f1,0)*Wx2'*s2;
    Wx2=Wx2-a*s2*a1';
    b2=b2-a*s2;
    Wx1=Wx1-a*s1*p';
    b1=b1-a*s1;
    % 换一个输入重新计算
    p=p+0.01;
    % 判断是否收敛，求整个区间的总的误差，类似均方误差，由于e有正有负，所以必须加其平方。
    if p>2.0
        fprintf('iteration: %d, E=%f\n',i,E);
        p=-2.0;
        if E<0.03
            flag=1;
        else
            E=0;
        end
        i=i+1;
    end
    E=E+e*e;
end
% 输出下结果
P=-2:0.1:2;
y=-2:0.1:2;
for i=1:41
    y(i)=purelin(Wx2*logsig(Wx1*P(i),b1)+b2);
end
T=1+sin((pi/4)*P);
plot(P,y); hold on ;plot(P,T)


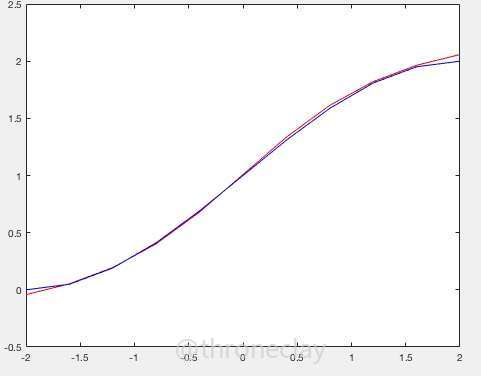
输出的结果如图，可以看到还是很好的收敛了，在书上看到这么一句话：在隐层神经元数量足够大的情况下，第一层采用sigmoid，第二层采用pureline的神经网络可以以任意精度逼近任意函数。